Por Danilo Eder Pinheiro Carvalho, Everaldo Lopes Carneiro, Gerinaldo Santos Ferreira e Marcos Franklin Mota Lima
 Matemático suiço, nascido na Basiléia, no último dia da segunda quinzena do primeiro quadrimestre do ano de 1707, filho de Paul Euler, Pastor Protestante, e Marguerite Brucker, descente de um pastor. Filho primogênito teve duas irmãs mais novas, Anna Maria e Maria Magdalena. Pouco depois do seu nascimento, sua família mudou-se para a cidade de Riehen, onde passou a maior parte da sua infância. Não aprendeu muito de Matemática na Escola, porém, através da convivência familiar, ganhou interesse e prazer pelo estudo da Matemática através dos ensinamentos do pai, estudando sozinho muitos livros de Matemática, chegando, inclusive, a procurar aulas particulares. Foi um menino precoce, dotado de excelente memória e grande facilidade para o aprendizado de línguas. Seu pai queria vê-lo seguir seus passos de pastoreio, razão pela qual matriculou Euler, ainda na adolescência, no ano de 1720, na Universidade de Basiléia para estudar Teologia. Em 1723, recebe o grau de Mestre em Filosofia com uma dissertação onde comparava Descartes com Newton. Nesse período já recebia, no fim de semana, lições de Johann Bernoulli que rapidamente descobriu o seu talento para a Matemática. Em 1726, Euler completou a sua dissertação na propagação do som.
Matemático suiço, nascido na Basiléia, no último dia da segunda quinzena do primeiro quadrimestre do ano de 1707, filho de Paul Euler, Pastor Protestante, e Marguerite Brucker, descente de um pastor. Filho primogênito teve duas irmãs mais novas, Anna Maria e Maria Magdalena. Pouco depois do seu nascimento, sua família mudou-se para a cidade de Riehen, onde passou a maior parte da sua infância. Não aprendeu muito de Matemática na Escola, porém, através da convivência familiar, ganhou interesse e prazer pelo estudo da Matemática através dos ensinamentos do pai, estudando sozinho muitos livros de Matemática, chegando, inclusive, a procurar aulas particulares. Foi um menino precoce, dotado de excelente memória e grande facilidade para o aprendizado de línguas. Seu pai queria vê-lo seguir seus passos de pastoreio, razão pela qual matriculou Euler, ainda na adolescência, no ano de 1720, na Universidade de Basiléia para estudar Teologia. Em 1723, recebe o grau de Mestre em Filosofia com uma dissertação onde comparava Descartes com Newton. Nesse período já recebia, no fim de semana, lições de Johann Bernoulli que rapidamente descobriu o seu talento para a Matemática. Em 1726, Euler completou a sua dissertação na propagação do som.Apesar de ser religioso, Leonhard não se entusiasmou com o estudo da teologia, e seu pai, por influência dos amigos matemáticos de seu filho, Nicolau e Daniel Bernoulli, filhos de um dos grandes matemáticos da época, Jean Bernoulli, foi persuadido a consentir que ele mudasse para a Matemática, o que de fato aconteceu e seu filho se tornou um grande matemático
Terminado o curso de Matemática, assumiu o posto de professor na Universidade de São Petersburgo, na Rússia, mantendo contato com grandes pensadores e cientistas a exemplo de Jakob Hermann, Daniel Bernoulli e Christian Goldbach. Euler recebeu uma instrução bastante ampla, pois além de Matemática, cursou Medicina, Astronomia, Física e Línguas Orientais.
No tempo de Euler os cientistas estavam mais presentes nas Academias de Ciências do que nas Universidades. As Academias contribuíram para a melhoria das Universidades, pois estas competiam com as academias pelos melhores talentos. A criação das academias e o fortalecimento das universidades se deveram ao espírito empreendedor dos grandes estadistas da época, a exemplo de Carlos II, na Inglaterra, Colbert, na França, Pedro, na Rússia, e Frederico II, na Prússia.
As academias eram centros de pesquisa científica e tecnológica, e contavam com boas instalações, aporte financeiro e plenas condições de funcionamento. Os pesquisadores e profissionais contratados tinham ampla liberdade em seus trabalhos e pesquisas, pois o que muito se esperava deles era que prestigiassem suas instituições com a publicação de pesquisas nos anais das academias as quais pertenciam. Entretanto, sempre que os governos precisavam, deveriam atender na solução de problemas nas diversas áreas como navegação, engenharia naval, hidráulica, acústica, cartografia, artes militares etc.
No ano de 1727 participou de competição premiada da Academia de Paris, na qual o problema a ser resolvido era encontrar a melhor maneira de colocar os mastros num navio. Ficou em segundo lugar, perdendo para aquele que mais tarde seria conhecido como “o pai da arquitetura naval”: Pierre Bouguer. Entretanto Euler ganharia o referido prêmio anual uma dúzia de vezes. Ainda no ano de 1727 ingressa nas forças armadas exercendo a função de Tenente da Marinha Russa. Deixou o posto no ano de 1730 para tornar-se professor de Física da Academia de Ciências. Já no ano de 1737, Euler assumiu o mais alto posto da hierarquia do magistério: a cátedra de matemática da Academia. Com a remuneração extra de tal conquista, encontrou as condições financeiras que lhe permitiram contrair matrimônio com Katharina Gsell, no ano de 1734. Tiveram treze filhos, mas, por falta de recursos da Medicina, apenas cinco sobreviveram à infância. O próprio Euler, ainda em vida, atribuiu a essa fase algumas de suas maiores descobertas científicas.
Após 1730 ele desenvolveu uma série de projetos acerca de cartografia, magnetismo, motores a combustão, máquinas e construção naval ... O foco da sua pesquisa estava agora bem definido: teoria de números; análises no infinito incluindo seus novos ramos, equações diferenciais e o cálculo de variações, e mecânica racional. Ele enxergava esses três campos como intimamente ligados. Estudos de teoria de números foram vitais para a fundamentação do cálculo, e funções especiais e equações diferenciais foram essenciais para mecânica racional, que fornecia problemas concretos.
O século XVIII, na História da Matemática, foi uma época de desenvolvimento do cálculo, de sistematização e aprimoramento de métodos. Muitos matemáticos viveram e produziram trabalhos importantes nesse século
São incontestáveis as contribuições de Euler para o seu e nosso tempo. No ano de 1735, Euler ganha fama mundial ao resolver um problema que por décadas foi desafio para os matemáticos da época. Trata-se da Série infinita da soma dos inversos dos quadrados dos números positivos, conhecido como problema da Basiléia, isto é a soma exata da série infinita.
A origem do nome do problema deve-se à cidade onde residia Euler Basileia, na qual também residia a família Bernoulli, que tentou solucionar o problema sem êxito.
Euler escreveu vários livros importantes para o ensino. Um deles é “A introdução à análise infinitesimal”, datado de 1748 e até hoje um texto de Cálculo admirado pela originalidade no trato de vários conceitos do Cálculo. É nesse livro que muitas das funções como logaritmos, exponenciais e as funções trigonométricas adquiriram a roupagem tal qual conhecemos hoje. Outra obra importante de Euler foi Cartas a uma jovem princesa, destinada à instrução da princesa Anhalt-Dessau, sobrinha de Frederico II, o Grande, versando sobre os mais variados assuntos científicos.
Leonhard Euler criou a mais ampla obra de matemática de todos os tempos, em todas as áreas da Matemática Pura e Aplicada. Álgebra, Geometria, Cálculo Infinitesimal, Teoria dos Números, Mecânica Racional, Mecânica Celeste, Geodésia, Cartografia, Balística e Hidrodinâmica são alguns domínios científicos deste gênio suíço chamado Euler.
Em Teoria dos números Euler é o maior nome que surgiu depois de Fermat. Integrou o Cálculo Diferencial de Leibnitz e o Método dos Fluxos de Newton à análise matemática. Euler criou o Cálculo das Variações que é o estudo das funcionais, ou funções que dependem de outras funções. Criou a Mecânica Analítica, cujos métodos têm um alcance maior dos que os métodos de Newton. Criou ainda a Geometria Diferencial, ou seja, um estudo das curvas e superfícies com métodos de Cálculo.
Ainda na Teoria dos Números enunciou o teorema dos números primos e a lei da reciprocidade biquadrática. Foi o mais prolífico escritor de Matemática de todos os tempos. Seu trabalho completo engloba 886 livros e artigos. Euler também foi responsável pela incorporação de numerosos símbolos à linguagem matemática: o “f(x)” das notações (1734); "e" para a base dos logaritmos naturais (1727); "i" para a raiz quadrada de -1 (1777); o símbolo "π” para o "pi"; o símbolo" ∑" para os somatórios (1755); a, b, e c para os lados de um triângulo e A, B e C para seus ângulos. Em 1765 propôs a solução para o problema das pontes de Konigsberg, sendo o fundador da "Teoria dos Grafos”, bastante utilizada na topografia
As funções e fórmulas de Euler são muito comuns na matemática. Duas das mais famosas são: e^(ix) = cos(x) + i sin(x) (quando x = ¼ nós temos ei¼ - 1 = 0 ), e V - A + F = 2 para qualquer poliedro simples com vértices, arestas e faces
Não se pode deixar de mencionar o famoso: "número de Euler" que permite várias simplificações no cálculo integral e logarítmico. Ele é o único número cuja derivada em x de e^x resulta em e^x.
Euler foi uma pessoa de grandes virtudes morais. Era homem simples e humilde. Teve em vida pleno reconhecimento de suas altas qualidades humanas e de grande cientista, por cujos trabalhos recebeu muitos prêmios. Foi um homem feliz, mas não escapou ao sofrimento imposto pela vida: começou a perder a visão do olho direito aos 31 anos de idade e logo ficou cego desse olho.
Em 1771, idoso e adoentado Euler experimentou uma tragédia em sua vida quando sua casa foi arrasada por um incêndio. Tudo o que conseguiu salvar foram seus valorosos manuscritos. Imbuído de sólida fé cristã, enfrentou todos esses embates sem perder o ânimo de continuar sua caminhada no tempo e sua sensacional produção científica. Segundo a História, como seqüela deste episódio de dor, Euler ficou totalmente cego, mas não parou de produzir. Continuou com seus projetos, e quase a metade de toda a sua produção científica foi concluída após esses incidentes. Euler contou com a ajuda valorosa de dois de seus filhos, Johann Albrecht Euler e Christoph Euler como também de dois membros da Academia.
Leonhard Euler veio a falecer em São Petersburgo, Rússia, no ano de 1783, no dia 18 de setembro, aos 76 anos, repentinamente quando tomava chá com um dos seus netos.
Euler escreveu vários livros importantes para o ensino. Um deles é “A introdução à análise infinitesimal”, datado de 1748 e até hoje um texto de Cálculo admirado pela originalidade no trato de vários conceitos do Cálculo. É nesse livro que muitas das funções como logaritmos, exponenciais e as funções trigonométricas adquiriram a roupagem tal qual conhecemos hoje. Outra obra importante de Euler foi Cartas a uma jovem princesa, destinada à instrução da princesa Anhalt-Dessau, sobrinha de Frederico II, o Grande, versando sobre os mais variados assuntos científicos.
Leonhard Euler criou a mais ampla obra de matemática de todos os tempos, em todas as áreas da Matemática Pura e Aplicada. Álgebra, Geometria, Cálculo Infinitesimal, Teoria dos Números, Mecânica Racional, Mecânica Celeste, Geodésia, Cartografia, Balística e Hidrodinâmica são alguns domínios científicos deste gênio suíço chamado Euler.
Em Teoria dos números Euler é o maior nome que surgiu depois de Fermat. Integrou o Cálculo Diferencial de Leibnitz e o Método dos Fluxos de Newton à análise matemática. Euler criou o Cálculo das Variações que é o estudo das funcionais, ou funções que dependem de outras funções. Criou a Mecânica Analítica, cujos métodos têm um alcance maior dos que os métodos de Newton. Criou ainda a Geometria Diferencial, ou seja, um estudo das curvas e superfícies com métodos de Cálculo.
Ainda na Teoria dos Números enunciou o teorema dos números primos e a lei da reciprocidade biquadrática. Foi o mais prolífico escritor de Matemática de todos os tempos. Seu trabalho completo engloba 886 livros e artigos. Euler também foi responsável pela incorporação de numerosos símbolos à linguagem matemática: o “f(x)” das notações (1734); "e" para a base dos logaritmos naturais (1727); "i" para a raiz quadrada de -1 (1777); o símbolo "π” para o "pi"; o símbolo" ∑" para os somatórios (1755); a, b, e c para os lados de um triângulo e A, B e C para seus ângulos. Em 1765 propôs a solução para o problema das pontes de Konigsberg, sendo o fundador da "Teoria dos Grafos”, bastante utilizada na topografia
As funções e fórmulas de Euler são muito comuns na matemática. Duas das mais famosas são: e^(ix) = cos(x) + i sin(x) (quando x = ¼ nós temos ei¼ - 1 = 0 ), e V - A + F = 2 para qualquer poliedro simples com vértices, arestas e faces
Não se pode deixar de mencionar o famoso: "número de Euler" que permite várias simplificações no cálculo integral e logarítmico. Ele é o único número cuja derivada em x de e^x resulta em e^x.
Euler foi uma pessoa de grandes virtudes morais. Era homem simples e humilde. Teve em vida pleno reconhecimento de suas altas qualidades humanas e de grande cientista, por cujos trabalhos recebeu muitos prêmios. Foi um homem feliz, mas não escapou ao sofrimento imposto pela vida: começou a perder a visão do olho direito aos 31 anos de idade e logo ficou cego desse olho.
Em 1771, idoso e adoentado Euler experimentou uma tragédia em sua vida quando sua casa foi arrasada por um incêndio. Tudo o que conseguiu salvar foram seus valorosos manuscritos. Imbuído de sólida fé cristã, enfrentou todos esses embates sem perder o ânimo de continuar sua caminhada no tempo e sua sensacional produção científica. Segundo a História, como seqüela deste episódio de dor, Euler ficou totalmente cego, mas não parou de produzir. Continuou com seus projetos, e quase a metade de toda a sua produção científica foi concluída após esses incidentes. Euler contou com a ajuda valorosa de dois de seus filhos, Johann Albrecht Euler e Christoph Euler como também de dois membros da Academia.
Leonhard Euler veio a falecer em São Petersburgo, Rússia, no ano de 1783, no dia 18 de setembro, aos 76 anos, repentinamente quando tomava chá com um dos seus netos.
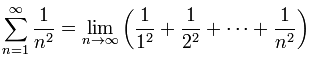
Nenhum comentário:
Postar um comentário
Deixe aqui sua contribuição para este blog. Ajude-nos a fazer deste veículo um instrumento de troca de experiências entre os professores de Matematica e outros profissionais da educação.